|
|
|
最小生成树问题,简称MST,指给定一个带权的无向连通图,如果选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树。
图有N个顶点,就一定有N-1条边,且必须包含所有顶点,所有边都在图中。解决最小生成树问题的算法主要有普利姆算法和克鲁斯卡尔算法。 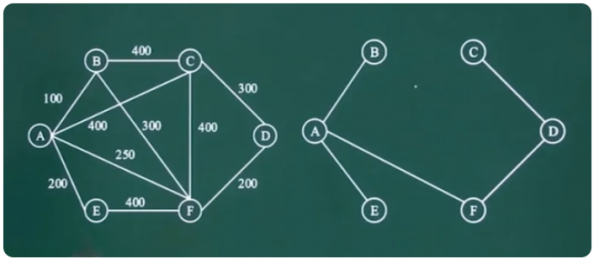
最小生成树算法,分别用C语言,C++,java,python编写出来
当涉及最小生成树算法时,可以使用多种编程语言来实现。以下是使用C语言、C++、Java和Python编写最小生成树算法的示例:
1.**C语言示例:**
- #include <stdio.h>
- #include <stdbool.h>
- #include <limits.h>
- #define V 5
- int minKey(int key[], bool mstSet[]) {
- int min = INT_MAX, min_index;
- for (int v = 0; v < V; v++) {
- if (mstSet[v] == false && key[v] < min) {
- min = key[v];
- min_index = v;
- }
- }
- return min_index;
- }
- void printMST(int parent[], int graph[V][V]) {
- printf("Edge \tWeight\n");
- for (int i = 1; i < V; i++) {
- printf("%d - %d \t%d \n", parent[i], i, graph[i][parent[i]]);
- }
- }
- void primMST(int graph[V][V]) {
- int parent[V];
- int key[V];
- bool mstSet[V];
- for (int i = 0; i < V; i++) {
- key[i] = INT_MAX;
- mstSet[i] = false;
- }
- key[0] = 0;
- parent[0] = -1;
- for (int count = 0; count < V - 1; count++) {
- int u = minKey(key, mstSet);
- mstSet[u] = true;
- for (int v = 0; v < V; v++) {
- if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
- parent[v] = u;
- key[v] = graph[u][v];
- }
- }
- }
- printMST(parent, graph);
- }
int graph[V][V] = {
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0}
};
primMST(graph);
return 0;
}
2.**C++示例:**
- #include <iostream>
- #include <climits>
- using namespace std;
- #define V 5
- int minKey(int key[], bool mstSet[]) {
- int min = INT_MAX, min_index;
- for (int v = 0; v < V; v++) {
- if (mstSet[v] == false && key[v] < min) {
- min = key[v];
- min_index = v;
- }
- }
- return min_index;
- }
- void printMST(int parent[], int graph[V][V]) {
- cout << "Edge \tWeight\n";
- for (int i = 1; i < V; i++) {
- cout << parent[i] << " - " << i << "\t" << graph[i][parent[i]] << endl;
- }
- }
- void primMST(int graph[V][V]) {
- int parent[V];
- int key[V];
- bool mstSet[V];
- for (int i = 0; i < V; i++) {
- key[i] = INT_MAX;
- mstSet[i] = false;
- }
- key[0] = 0;
- parent[0] = -1;
- for (int count = 0; count < V - 1; count++) {
- int u = minKey(key, mstSet);
- mstSet[u] = true;
- for (int v = 0; v < V; v++) {
- if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
- parent[v] = u;
- key[v] = graph[u][v];
- }
- }
- }
- printMST(parent, graph);
- }
int graph[V][V] = {
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0}
};
primMST(graph);
return 0;
}
3.**Java示例:**
- import java.util.Arrays;
- class MST {
- private static final int V = 5;
- int minKey(int key[], Boolean mstSet[]) {
- int min = Integer.MAX_VALUE, min_index = -1;
- for (int v = 0; v < V; v++) {
- if (mstSet[v] == false && key[v] < min) {
- min = key[v];
- min_index = v;
- }
- }
- return min_index;
- }
- void printMST(int parent[], int graph[][]) {
- System.out.println("Edge \tWeight");
- for (int i = 1; i < V; i++) {
- System.out.println(parent[i] + " - " + i + "\t" + graph[i][parent[i]]);
- }
- }
- void primMST(int graph[][]) {
- int parent[] = new int[V];
- int key[] = new int[V];
- Boolean mstSet[] = new Boolean[V];
- Arrays.fill(key, Integer.MAX_VALUE);
- Arrays.fill(mstSet, false);
- key[0] = 0;
- parent[0] = -1;
- for (int count = 0; count < V - 1; count++) {
- int u = minKey(key, mstSet);
- mstSet[u] = true;
- for (int v = 0; v < V; v++) {
- if (graph[u][v] != 0 && mstSet[v] == false && graph[u][v] < key[v]) {
- parent[v] = u;
- key[v] = graph[u][v];
- }
- }
- }
- printMST(parent, graph);
- }
-
- }
int graph[][] = {
{ 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 }
};
MST mst = new MST();
mst.primMST(graph);
}
4.**Python示例:**
- class MST:
- def __init__(self, vertices):
- self.V = vertices
- self.graph = [[0 for _ in range(vertices)] for _ in range(vertices)]
- def minKey(self, key, mstSet):
- min = float("inf")
- min_index = -1
- for v in range(self.V):
- if key[v] < min and mstSet[v] == False:
- min = key[v]
- min_index = v
- return min_index
- def printMST(self, parent):
- print("Edge \tWeight")
- for i in range(1, self.V):
- print(parent[i], "-", i, "\t", self.graph[i][parent[i]])
- def primMST(self):
- key = [float("inf")] * self.V
- parent = [None] * self.V
- mstSet = [False] * self.V
- key[0] = 0
- parent[0] = -1
- for _ in range(self.V - 1):
- u = self.minKey(key, mstSet)
- mstSet[u] = True
- for v in range(self.V):
- if (
- self.graph[u][v] > 0
- and mstSet[v] == False
- and key[v] > self.graph[u][v]
- ):
- key[v] = self.graph[u][v]
- parent[v] = u
- self.printMST(parent)
graph = [
[0, 2, 0, 6, 0],
[2, 0, 3, 8, 5],
[0, 3, 0, 0, 7],
[6, 8, 0, 0, 9],
[0, 5, 7, 9, 0],
]
mst = MST(5)
mst.graph = graph
mst.primMST()
这些示例展示了使用不同编程语言实现最小生成树算法。每个示例都使用了类似的思路,通过选择最小权重的边来构建最小生成树。您可以根据需要修改算法和输入图形。请注意,这只是最小生成树算法的简单示例,实际应用中可能会有更复杂的问题和算法。

扫码关注微信公众号,免费查看完整算法内容。 |
|
|
|
|